TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI
TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.
FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
-
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......
ΤDCG
X
Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli +
DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
-
-
DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
x
sistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].
x
número atômico, estrutura eletrônica, níveis de energia
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
-
T l T l E l Fl dfG l
X
TODA FORMA DE FUNÇÃO E EQUAÇÃO EM:
Em física estatística e física da matéria condensada, densidade de estados (DOS, do inglês density of states) é a propriedade que quantifica quão proximamente "empacotado" em níveis de energia está um sistema mecânico quântico. Um DOS alto em um nível específico de energia significa que há muitos estados disponíveis para ocupação. Um DOS nulo, zero, significa que nenhum estado pode ser ocupado em um nível de energia.
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
número atômico, estrutura eletrônica, níveis de energia
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
X
TODA FORMA DE FUNÇÃO E EQUAÇÃO EM:
Em física estatística e física da matéria condensada, densidade de estados (DOS, do inglês density of states) é a propriedade que quantifica quão proximamente "empacotado" em níveis de energia está um sistema mecânico quântico. Um DOS alto em um nível específico de energia significa que há muitos estados disponíveis para ocupação. Um DOS nulo, zero, significa que nenhum estado pode ser ocupado em um nível de energia.
Índice
Explanação[editar | editar código-fonte]
Ondas, partículas comportando-se como ondas, podem somente existir dentro de sistemas mecânico quânticos (MQ) se propriedades do sistema seguem a ondulação existente. Em alguns sistemas, o espaçamento interatômico e a carga atômica do material segue somente elétrons de certos comprimento de onda existentes. Em outros sistemas. a estrutura cristalina do material leva ondas a se propagar em somente uma direção, enquanto suprime a propagação de ondas em outra direção. Ondas em um sistema MQ tem comprimentos de onda específicos e podem propagar-se em direções específicas, e cada onda ocupa um diferente modo,ou estado. Devido a muitos destes estados terem o mesmos comprimentos de onda, entretanto dividirem a mesma energia, podem existir muitos estados disponíveis em certos níveis de energia, enquanto nenhum estado é disponível em outros níveis de energia.
Por exemplo, a densidade de estados para elétrons em um semicondutor é mostrada em vermelho na Fig. 2. Para elétrons na fronteira da faixa de condução, muito poucos estados estão disponíveis para o elétron ocupar. A medida que o elétron aumenta em energia, a densidade de estados do elétron aumenta e mais estados tornam-se disponíveis para ocupação. Entretanto, porque não há estados disponíveis para elétrons ocuparem dentro da faixa de abertura, elétrons na fronteira da faixa de condução devem perder pelo menos de energia de maneira a realizarem a transição a outro estado disponível.
A densidade de estados pode ser calculada para elétrons, fótons, ou fónons em sistemas MQ. É usualmente notado com um dos símbolos g, , n, ou N. É uma função g(E) da energia interna E, na qual a expressão g(E) dE representa o número de estado com energias entre E e E+dE.
Para converter entre energia e vetor de onda, a relação específica entre E e k deve ser conhecida. Por exemplo, a fórmula para elétrons é
E para fótons, a fórmula é
Pode também ser escrito como uma função da frequência angular , a qual é proporcional à energia. A densidade de estados é usada extensivamente em física da matéria condensada, onde pode referir-se ao nível de energia dos elétrons, fótons ou fônons em um sólido cristalino. Em sólidos cristalinos, há frequentemente níveis de energia onde a densidade dos estados dos elétrons é zero, o que significa que os elétrons não podem ser excitados a estas energias. A densidade dos estados também ocorre na regra dourada de Fermi, a qual descreve quão rápido as transições mecânico quânticas ocorrem na presença de uma perturbação.
Num sistema tridimensional, a densidade de estados em espaço recíproco (espaço k) é
onde V é o volume e n o número de pontos de ramificação que existem para um único valor de k. Estes pontos de ramificação são por exemplo o spin-acima e spin-abaixo estados para elétrons, as polarizações de fótons, e os modos longitudinais ou transversais para fônons.
Ondas, partículas comportando-se como ondas, podem somente existir dentro de sistemas mecânico quânticos (MQ) se propriedades do sistema seguem a ondulação existente. Em alguns sistemas, o espaçamento interatômico e a carga atômica do material segue somente elétrons de certos comprimento de onda existentes. Em outros sistemas. a estrutura cristalina do material leva ondas a se propagar em somente uma direção, enquanto suprime a propagação de ondas em outra direção. Ondas em um sistema MQ tem comprimentos de onda específicos e podem propagar-se em direções específicas, e cada onda ocupa um diferente modo,ou estado. Devido a muitos destes estados terem o mesmos comprimentos de onda, entretanto dividirem a mesma energia, podem existir muitos estados disponíveis em certos níveis de energia, enquanto nenhum estado é disponível em outros níveis de energia.
Por exemplo, a densidade de estados para elétrons em um semicondutor é mostrada em vermelho na Fig. 2. Para elétrons na fronteira da faixa de condução, muito poucos estados estão disponíveis para o elétron ocupar. A medida que o elétron aumenta em energia, a densidade de estados do elétron aumenta e mais estados tornam-se disponíveis para ocupação. Entretanto, porque não há estados disponíveis para elétrons ocuparem dentro da faixa de abertura, elétrons na fronteira da faixa de condução devem perder pelo menos de energia de maneira a realizarem a transição a outro estado disponível.
A densidade de estados pode ser calculada para elétrons, fótons, ou fónons em sistemas MQ. É usualmente notado com um dos símbolos g, , n, ou N. É uma função g(E) da energia interna E, na qual a expressão g(E) dE representa o número de estado com energias entre E e E+dE.
Para converter entre energia e vetor de onda, a relação específica entre E e k deve ser conhecida. Por exemplo, a fórmula para elétrons é
E para fótons, a fórmula é
Pode também ser escrito como uma função da frequência angular , a qual é proporcional à energia. A densidade de estados é usada extensivamente em física da matéria condensada, onde pode referir-se ao nível de energia dos elétrons, fótons ou fônons em um sólido cristalino. Em sólidos cristalinos, há frequentemente níveis de energia onde a densidade dos estados dos elétrons é zero, o que significa que os elétrons não podem ser excitados a estas energias. A densidade dos estados também ocorre na regra dourada de Fermi, a qual descreve quão rápido as transições mecânico quânticas ocorrem na presença de uma perturbação.
Num sistema tridimensional, a densidade de estados em espaço recíproco (espaço k) é
onde V é o volume e n o número de pontos de ramificação que existem para um único valor de k. Estes pontos de ramificação são por exemplo o spin-acima e spin-abaixo estados para elétrons, as polarizações de fótons, e os modos longitudinais ou transversais para fônons.
Materiais cristalinos[editar | editar código-fonte]
Dado que em materiais (cristalinos), o número de escalas varia linearmente com o volume, uma diferente definição de densidade de estados é algumas vezes usada, na qual g(E) ou g(k) é o número de estados por unidade de energia (vetor onda) e por unidade de volume ou por unidade de célula da grade.
Em um material cristalino, onde os estados mecânico quânticos podem ser descritos em termos de seus vetores de onda k, a densidade dos estados como uma função de k é não dependente das propriedades do material. Das condições periódicas segue que em um volume arbitrário , somente vetores k são mantidos satisfazendo
onde são inteiros positivos ou negativos arbitrários. Usando
pode ser derivado que para uma matriz tridimensional o número de estados G(k) dk entre k e k+dk é
para um único caso.
Em sólidos, a relação entre E e k é geralmente muito complexa e dependente do material. Se a relação é conhecida, a expressão para a densidade dos estados é
A relação acima é somente significativa se a energia somente depende da manitude do vetor k.
O modelo XY clássico (às vezes também chamado de modelo clássico de rotor ou modelo O(2)) é um modelo de rede diagonal de mecânica estatística. É o caso especial do modelo vetorial n para .[1][2]
Dado que em materiais (cristalinos), o número de escalas varia linearmente com o volume, uma diferente definição de densidade de estados é algumas vezes usada, na qual g(E) ou g(k) é o número de estados por unidade de energia (vetor onda) e por unidade de volume ou por unidade de célula da grade.
Em um material cristalino, onde os estados mecânico quânticos podem ser descritos em termos de seus vetores de onda k, a densidade dos estados como uma função de k é não dependente das propriedades do material. Das condições periódicas segue que em um volume arbitrário , somente vetores k são mantidos satisfazendo
onde são inteiros positivos ou negativos arbitrários. Usando
pode ser derivado que para uma matriz tridimensional o número de estados G(k) dk entre k e k+dk é
para um único caso.
Em sólidos, a relação entre E e k é geralmente muito complexa e dependente do material. Se a relação é conhecida, a expressão para a densidade dos estados é
A relação acima é somente significativa se a energia somente depende da manitude do vetor k.
O modelo XY clássico (às vezes também chamado de modelo clássico de rotor ou modelo O(2)) é um modelo de rede diagonal de mecânica estatística. É o caso especial do modelo vetorial n para .[1][2]
Definição[editar | editar código-fonte]
Dada uma rede diagonal Λ dimensional-D, para cada sítio j ∈ Λ da rede existe um vetor de comprimento unitário bidimensional sj = (cos θj, sin θj)
A configuração de rotação, s = (sj)j ∈ Λ é uma atribuição do ângulo −π < θj ≤ π para cada j ∈ Λ.
Dada uma tradução invariante da interação Jij = J(i − j) e um campo externo dependente do ponto , a energia de configuração é
O caso em que Jij = 0, exceto para o vizinho mais próximo ij, é chamado de "caso do vizinho mais próximo".
A probabilidade de configuração é dada pela distribuição de Boltzmann com temperatura inversa β ≥ 0:
onde Z é a normalização ou função de partição.[3] A notação indica a expectativa da variável aleatória A(s) no limite de volume infinito, após as condições de fronteira periódicas terem sido impostas.
Dada uma rede diagonal Λ dimensional-D, para cada sítio j ∈ Λ da rede existe um vetor de comprimento unitário bidimensional sj = (cos θj, sin θj)
A configuração de rotação, s = (sj)j ∈ Λ é uma atribuição do ângulo −π < θj ≤ π para cada j ∈ Λ.
Dada uma tradução invariante da interação Jij = J(i − j) e um campo externo dependente do ponto , a energia de configuração é
O caso em que Jij = 0, exceto para o vizinho mais próximo ij, é chamado de "caso do vizinho mais próximo".
A probabilidade de configuração é dada pela distribuição de Boltzmann com temperatura inversa β ≥ 0:
onde Z é a normalização ou função de partição.[3] A notação indica a expectativa da variável aleatória A(s) no limite de volume infinito, após as condições de fronteira periódicas terem sido impostas.
Afinidade eletrônica em matéria condensada[editar | editar código-fonte]
Ao lidarmos com física do estado sólido e ao considerarmos técnicas de análise como a Espectroscopia de fotoelétrons excitados por raios X,[2] a afinidade eletrônica é definida como a energia que seria liberada caso um elétron com energia de vácuo fosse introduzido na amostra, inicialmente neutra, ficando o mesmo por esta confinado. Sendo ENTotal a energia total do sistema com N+1 elétrons, N na amostra, neutra e em seu equilíbrio termodinâmico, e EN+1Total a energia total do sistema em seu novo equilíbrio termodinâmico após a admissão do elétron, antes estático ao nível de vácuo, e após a liberação da energia envolvida no processo de admissão, temos:
-
- χ = ENTotal − EN+1Total
Um elétron, ao ser introduzido no sólido, deve ocupar, assumindo o equilíbrio termodinâmico, o primeiro estado disponível em energia, ou seja, o estado desocupado com menor energia na banda de condução. A eletroafinidade corresponde portanto à diferença de energias entre o nível de vácuo e a energia do primeiro estado livre, o menos energético dentro da banda de condução do sólido. No caso de metais, equipara-se à energia de Fermi. Em semicondutores, corresponde à diferença de energias entre o nível de vácuo e a energia mínima da banda de condução.
O efeito Hall está relacionado ao surgimento de uma diferença de potencial em um condutor elétrico, transversal ao fluxo de corrente e um campo magnético perpendicular à corrente. Esse fenômeno, descoberto em 1879 por Edwin Herbert Hall,[1] é extremamente importante no estudo da condutividade, pois a partir do coeficiente de Hall é possível determinar o sinal e a densidade de portadores de carga em diferentes tipos de materiais. O efeito Hall é a base de diversos métodos experimentais utilizados na caracterização de metais e semicondutores.
Ao lidarmos com física do estado sólido e ao considerarmos técnicas de análise como a Espectroscopia de fotoelétrons excitados por raios X,[2] a afinidade eletrônica é definida como a energia que seria liberada caso um elétron com energia de vácuo fosse introduzido na amostra, inicialmente neutra, ficando o mesmo por esta confinado. Sendo ENTotal a energia total do sistema com N+1 elétrons, N na amostra, neutra e em seu equilíbrio termodinâmico, e EN+1Total a energia total do sistema em seu novo equilíbrio termodinâmico após a admissão do elétron, antes estático ao nível de vácuo, e após a liberação da energia envolvida no processo de admissão, temos:
-
- χ = ENTotal − EN+1Total
Um elétron, ao ser introduzido no sólido, deve ocupar, assumindo o equilíbrio termodinâmico, o primeiro estado disponível em energia, ou seja, o estado desocupado com menor energia na banda de condução. A eletroafinidade corresponde portanto à diferença de energias entre o nível de vácuo e a energia do primeiro estado livre, o menos energético dentro da banda de condução do sólido. No caso de metais, equipara-se à energia de Fermi. Em semicondutores, corresponde à diferença de energias entre o nível de vácuo e a energia mínima da banda de condução.
O efeito Hall está relacionado ao surgimento de uma diferença de potencial em um condutor elétrico, transversal ao fluxo de corrente e um campo magnético perpendicular à corrente. Esse fenômeno, descoberto em 1879 por Edwin Herbert Hall,[1] é extremamente importante no estudo da condutividade, pois a partir do coeficiente de Hall é possível determinar o sinal e a densidade de portadores de carga em diferentes tipos de materiais. O efeito Hall é a base de diversos métodos experimentais utilizados na caracterização de metais e semicondutores.
Índice
Descoberta[editar | editar código-fonte]
Em 1879 Edwin Herbert Hall descobriu o efeito que leva seu nome durante seu doutorado em física sob a supervisão de Henry Augustus Rowland na Universidade Johns Hopkins em Baltimore, Maryland. Durante seus estudos experimentais sobre a influência do campo magnético nos portadores de carga da corrente elétrica ele determinou a existência de portadores de carga negativa muitos anos antes da descoberta dos elétrons por Joseph John Thomson. Ele descobriu que um campo magnético desviaria o movimento de cargas eletrônicas dentro de um condutor e que a quantidade de deflexão pode ser medida como uma voltagem perpendicular ao fluxo de carga, essa voltagem também é conhecida como voltagem Hall, que revela as informações essenciais sobre os portadores de carga em um semicondutor, incluindo se são elétrons negativos ou quase partículas positivas, sua velocidade em um campo elétrico ou sua “mobilidade” (µ) e sua densidade (n) dentro do semicondutor.[2]
Em 1879 Edwin Herbert Hall descobriu o efeito que leva seu nome durante seu doutorado em física sob a supervisão de Henry Augustus Rowland na Universidade Johns Hopkins em Baltimore, Maryland. Durante seus estudos experimentais sobre a influência do campo magnético nos portadores de carga da corrente elétrica ele determinou a existência de portadores de carga negativa muitos anos antes da descoberta dos elétrons por Joseph John Thomson. Ele descobriu que um campo magnético desviaria o movimento de cargas eletrônicas dentro de um condutor e que a quantidade de deflexão pode ser medida como uma voltagem perpendicular ao fluxo de carga, essa voltagem também é conhecida como voltagem Hall, que revela as informações essenciais sobre os portadores de carga em um semicondutor, incluindo se são elétrons negativos ou quase partículas positivas, sua velocidade em um campo elétrico ou sua “mobilidade” (µ) e sua densidade (n) dentro do semicondutor.[2]
Teoria[editar | editar código-fonte]
Durante seus estudos de doutorado, Edwin Hall buscava entender qual a influência de um campo magnético externo sob um fio condutor. Ele queria entender se a força devido a este campo externo atuaria sobre os portadores de corrente elétrica ou sobre o fio como um todo. Hall acreditava que essa força magnética atuaria sobre os portadores de carga fazendo com que a corrente se deslocasse para uma determinada região do fio, e portanto, a resistência do fio iria aumentar. Apesar de não observar tal aumento na resistência do fio em seus experimentos, Hall sabia que de alguma forma a corrente elétrica era alterada sem que a resistência fosse modificada. Ele propôs a presença de um estado de stress em uma determinada região do condutor, devido ao acúmulo de portadores de carga, que originaria uma diferença de potencial transversal mais tarde conhecida como tensão de Hall.
Para entender melhor a origem desse fenômeno vamos considerar a definição para corrente elétrica segundo o modelo de Drude, ou seja, vamos considerar que a corrente é formada por um fluxo de portadores de carga (elétrons, íons ou lacunas) que seguem uma trajetória linear até que se choquem com os átomos da rede, impurezas, fônons, etc. Em seus experimentos, Hall considerou um fio metálico conduzindo corrente elétrica ao longo do eixo x (com densidade de corrente ), sob a ação de um campo magnético externo aplicado ao longo do eixo z. A presença do campo faz com que os portadores de carga experimentem uma força magnética que causa uma deflexão na trajetória dos portadores na direção y. Essa mudança de trajetória gera um gradiente de cargas e consequentemente surge um campo elétrico na direção y , conhecido como campo de Hall. Devido as dimensões finitas do fio haverá um acúmulo de cargas nas extremidades ao longo da direção y, resultando em uma diferença de potencial conhecida como potencial de Hall, . Para um metal simples, ou seja, com um único portador de carga, o potencial de Hall pode ser escrito como:
Onde representa a densidade de portadores e a espessura do fio. Uma outra quantidade interessante relacionada ao efeito Hall é o coeficiente de Hall, que é a constante de proporcionalidade entre o campo de Hall e o produto do campo magnético com o fluxo de corrente
Como o sinal da força magnética é o mesmo para cargas positivas se movendo em uma determinada direção e cargas negativas se movendo na direção oposta, o sinal do coeficiente de Hall depende exclusivamente do campo de Hall. Assim, como o sinal de depende exclusivamente do sinal da carga dos portadores, o coeficiente de Hall permite identificar se o fluxo de corrente se deve a portadores negativos () ou positivos (). Desta maneira, podemos concluir que o efeito Hall, além de permitir a determinação da densidade de corrente e a mobilidade dos portadores ou do campo magnético, este também permite a distinção entre um fluxo de cargas positivas e negativas. O efeito Hall é a primeira prova real de que a corrente elétrica em metais se deve ao movimento dos elétrons e não dos prótons. Ainda mais, esse efeito demonstrou que em alguns materiais, especialmente semicondutores do tipo p, a maneira mais apropriada de se descrever a corrente elétrica é através do fluxo de buracos positivos ao invés de elétrons. Contudo, o efeito Hall gera confusões em alguns casos, por exemplo, buracos se movendo para a esquerda na realidade são elétrons se movendo para a direita e portanto devemos ter o mesmo sinal para o coeficiente de Hall, o que não ocorre. Tal problema só pode ser solucionado quando consideramos a teoria quântica do transporte em sólidos [2].
Durante seus estudos de doutorado, Edwin Hall buscava entender qual a influência de um campo magnético externo sob um fio condutor. Ele queria entender se a força devido a este campo externo atuaria sobre os portadores de corrente elétrica ou sobre o fio como um todo. Hall acreditava que essa força magnética atuaria sobre os portadores de carga fazendo com que a corrente se deslocasse para uma determinada região do fio, e portanto, a resistência do fio iria aumentar. Apesar de não observar tal aumento na resistência do fio em seus experimentos, Hall sabia que de alguma forma a corrente elétrica era alterada sem que a resistência fosse modificada. Ele propôs a presença de um estado de stress em uma determinada região do condutor, devido ao acúmulo de portadores de carga, que originaria uma diferença de potencial transversal mais tarde conhecida como tensão de Hall.
Para entender melhor a origem desse fenômeno vamos considerar a definição para corrente elétrica segundo o modelo de Drude, ou seja, vamos considerar que a corrente é formada por um fluxo de portadores de carga (elétrons, íons ou lacunas) que seguem uma trajetória linear até que se choquem com os átomos da rede, impurezas, fônons, etc. Em seus experimentos, Hall considerou um fio metálico conduzindo corrente elétrica ao longo do eixo x (com densidade de corrente ), sob a ação de um campo magnético externo aplicado ao longo do eixo z. A presença do campo faz com que os portadores de carga experimentem uma força magnética que causa uma deflexão na trajetória dos portadores na direção y. Essa mudança de trajetória gera um gradiente de cargas e consequentemente surge um campo elétrico na direção y , conhecido como campo de Hall. Devido as dimensões finitas do fio haverá um acúmulo de cargas nas extremidades ao longo da direção y, resultando em uma diferença de potencial conhecida como potencial de Hall, . Para um metal simples, ou seja, com um único portador de carga, o potencial de Hall pode ser escrito como:
Onde representa a densidade de portadores e a espessura do fio. Uma outra quantidade interessante relacionada ao efeito Hall é o coeficiente de Hall, que é a constante de proporcionalidade entre o campo de Hall e o produto do campo magnético com o fluxo de corrente
Como o sinal da força magnética é o mesmo para cargas positivas se movendo em uma determinada direção e cargas negativas se movendo na direção oposta, o sinal do coeficiente de Hall depende exclusivamente do campo de Hall. Assim, como o sinal de depende exclusivamente do sinal da carga dos portadores, o coeficiente de Hall permite identificar se o fluxo de corrente se deve a portadores negativos () ou positivos (). Desta maneira, podemos concluir que o efeito Hall, além de permitir a determinação da densidade de corrente e a mobilidade dos portadores ou do campo magnético, este também permite a distinção entre um fluxo de cargas positivas e negativas. O efeito Hall é a primeira prova real de que a corrente elétrica em metais se deve ao movimento dos elétrons e não dos prótons. Ainda mais, esse efeito demonstrou que em alguns materiais, especialmente semicondutores do tipo p, a maneira mais apropriada de se descrever a corrente elétrica é através do fluxo de buracos positivos ao invés de elétrons. Contudo, o efeito Hall gera confusões em alguns casos, por exemplo, buracos se movendo para a esquerda na realidade são elétrons se movendo para a direita e portanto devemos ter o mesmo sinal para o coeficiente de Hall, o que não ocorre. Tal problema só pode ser solucionado quando consideramos a teoria quântica do transporte em sólidos [2].
Efeito Hall em semicondutores[editar | editar código-fonte]
A forma do coeficiente de Hall para semicondutores é mais complexa, uma vez que podemos ter dois tipos de portadores de carga, elétrons e buracos, com densidades e mobilidades diferentes. Para o caso de campos magnéticos moderados podemos escrever o coeficiente de Hall como sendo [3]
onde e são as densidades e e são as mobilidades para os elétrons e buracos respectivamente. No caso de campos magnéticos altos o coeficiente de Hall é análogo ao caso de um único portador
onde .
A forma do coeficiente de Hall para semicondutores é mais complexa, uma vez que podemos ter dois tipos de portadores de carga, elétrons e buracos, com densidades e mobilidades diferentes. Para o caso de campos magnéticos moderados podemos escrever o coeficiente de Hall como sendo [3]
onde e são as densidades e e são as mobilidades para os elétrons e buracos respectivamente. No caso de campos magnéticos altos o coeficiente de Hall é análogo ao caso de um único portador
onde .
Efeito Hall quântico[editar | editar código-fonte]
Ver artigo principal: Quantum Hall Effect (em inglês)
Efeito observado em sistemas eletrônicos de duas dimensões sob baixas temperaturas e altos campos magnéticos. A característica marcante desse efeito é a presença de uma condutividade de Hall quantizada, onde a quantização esta relacionada aos níveis de Landau.
Ver artigo principal: Quantum Hall Effect (em inglês)
Efeito observado em sistemas eletrônicos de duas dimensões sob baixas temperaturas e altos campos magnéticos. A característica marcante desse efeito é a presença de uma condutividade de Hall quantizada, onde a quantização esta relacionada aos níveis de Landau.
Efeito Hall com spin[editar | editar código-fonte]
Ver artigo principal: Spin Hall Effect (em inglês)
O efeito Hall com spin esta relacionado com a existência de um acúmulo de spin nas extremidades de um condutor com uma corrente de portadores. Neste caso, não é necessária a presença de um campo magnético externo para se observar o efeito. Esse efeito foi descoberto por I. Dyakonov e V.I.Perel, em 1971, e observado experimentalmente 30 anos mais tarde em semicondutores e metais sob criogenia e à temperatura ambiente.
Ver artigo principal: Spin Hall Effect (em inglês)
O efeito Hall com spin esta relacionado com a existência de um acúmulo de spin nas extremidades de um condutor com uma corrente de portadores. Neste caso, não é necessária a presença de um campo magnético externo para se observar o efeito. Esse efeito foi descoberto por I. Dyakonov e V.I.Perel, em 1971, e observado experimentalmente 30 anos mais tarde em semicondutores e metais sob criogenia e à temperatura ambiente.
Efeito Hall quântico com spin[editar | editar código-fonte]
Ver artigo principal: Quantum Spin Hall Effect (em inglês)
Observados em semicondutores de duas dimensões onde ocorre o acoplamento spin-órbita.
Ver artigo principal: Quantum Spin Hall Effect (em inglês)
Observados em semicondutores de duas dimensões onde ocorre o acoplamento spin-órbita.
Efeito Hall anômalo[editar | editar código-fonte]
Em materiais ferromagnéticos (e materiais paramagnéticos na presença de um campo magnético), a resistividade Hall inclui uma contribuição adicional ao efeito Hall comum, conhecido como o efeito Hall anômalo. Esse efeito depende diretamente da magnetização do material, e é frequentemente maior que o efeito Hall comum. Embora este seja um fenômeno bem conhecido, ainda existem discussões sobre sua origem em diversos materiais. O efeito Hall anômalo pode ser um efeito extrínseco causado pelo espalhamento dos portadores de carga com spin, ou um efeito intrínseco que pode ser descrito em termos do efeito de Fase de Berry no espaço dos momentum do cristal [5].
Em materiais ferromagnéticos (e materiais paramagnéticos na presença de um campo magnético), a resistividade Hall inclui uma contribuição adicional ao efeito Hall comum, conhecido como o efeito Hall anômalo. Esse efeito depende diretamente da magnetização do material, e é frequentemente maior que o efeito Hall comum. Embora este seja um fenômeno bem conhecido, ainda existem discussões sobre sua origem em diversos materiais. O efeito Hall anômalo pode ser um efeito extrínseco causado pelo espalhamento dos portadores de carga com spin, ou um efeito intrínseco que pode ser descrito em termos do efeito de Fase de Berry no espaço dos momentum do cristal [5].
Efeito Hall em gases ionizados[editar | editar código-fonte]
O efeito Hall em um gás ionizado (plasma) é significativamente diferente do efeito Hall em sólidos (onde o coeficiente de Hall é sempre muito inferior à unidade). Em um plasma, o coeficiente de Hall pode assumir qualquer valor. O coeficiente de Hall, em um plasma é a relação entre a girofrequência do elétron, , e a frequência de colisão entre os elétrons e as partículas pesadas ,
onde é a massa do elétron.
O valor do coeficiente de Hall é diretamente proporcional à intensidade do campo magnético. Fisicamente, sabemos que a trajetória dos elétrons é curvadas pela força magnética. No entanto, quando o coeficiente de Hall é baixo, o movimento entre os duas colisões com as partículas pesadas é quase linear. Mas, se o coeficiente de Hall é alto, a trajetória dos elétrons é altamente curvada. No caso do gás ionizado o vetor densidade de corrente não é mais colinear ao vetor campo elétrico, e o ângulo entre eles esta relacionado ao coeficiente de Hall da seguinte maneira
- .
-
A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação EF, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.
O efeito Hall em um gás ionizado (plasma) é significativamente diferente do efeito Hall em sólidos (onde o coeficiente de Hall é sempre muito inferior à unidade). Em um plasma, o coeficiente de Hall pode assumir qualquer valor. O coeficiente de Hall, em um plasma é a relação entre a girofrequência do elétron, , e a frequência de colisão entre os elétrons e as partículas pesadas ,
onde é a massa do elétron.
O valor do coeficiente de Hall é diretamente proporcional à intensidade do campo magnético. Fisicamente, sabemos que a trajetória dos elétrons é curvadas pela força magnética. No entanto, quando o coeficiente de Hall é baixo, o movimento entre os duas colisões com as partículas pesadas é quase linear. Mas, se o coeficiente de Hall é alto, a trajetória dos elétrons é altamente curvada. No caso do gás ionizado o vetor densidade de corrente não é mais colinear ao vetor campo elétrico, e o ângulo entre eles esta relacionado ao coeficiente de Hall da seguinte maneira
- .
- A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação EF, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.
Índice
Introdução[editar | editar código-fonte]
Contexto geral[editar | editar código-fonte]
-
A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.
A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.
Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.
Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.
A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:
onde εF é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, εF/k. Esta temperatura característica é da ordem de 105K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.
-
-
-
-
A flexoeletricidade é uma propriedade de um material dielétrico, pelo qual exibe uma polarização elétrica espontânea induzida por um gradiente de deformação.[1] A flexoeletricidade está intimamente relacionada à piezoeletricidade, mas enquanto a piezoeletricidade se refere à polarização devido à tensão uniforme, a flexoeletricidade se refere especificamente à polarização devido à tensão que muda de um ponto para outro no material.[2] Flexoeletricidade não é o mesmo que Ferroelasticidade[3].
A polarização elétrica devido ao estresse mecânico em um dielétrico é dada por:
onde o primeiro termo corresponde ao efeito piezoelétrico direto e o segundo termo corresponde à polarização flexoelétrica induzida pelo gradiente de deformação.
Aqui, o coeficiente flexoelétrico, , é um tensor polar de quarta ordem e é o coeficiente correspondente ao efeito piezoelétrico direto.
-
-
-
-
-
Denomina-se matéria degenerada, ou ainda gás degenerado, aquela na qual uma fração importante da pressão provém do princípio de exclusão de Pauli, que estabelece que dois férmions não podem ter os mesmos números quânticos.
Tal "gás" não obedece às leis clássicas segundo as quais a pressão de um gás é proporcional à sua temperatura e densidade.
Enrico Fermi e Paul Adrien Maurice Dirac provaram que, a uma densidade muito alta, a pressão aumenta rapidamente até o ponto em que ela passa a independer da temperatura do gás. Neste ponto, o gás passa a agir quase como um sólido.
Na astronomia, este gás é encontrado nas estrelas anãs brancas e é importante no tratamento tanto de estrelas residuais densas quanto das novas que as geram.[1] É conceito importante em cosmologia e na evolução do universo no tempo,[2] com relações com a teoria da relatividade[3] e para o modelo "big bang" e na detecção de objetos estelares.[4]
Dependendo das condições, a degeneração de diferentes partículas pode contribuir com a pressão de um objeto compacto, de modo que uma anã branca está sustentada pela degeneração dos elétrons, ainda que uma estrela de nêutrons não colapse devido ao efeito combinado da pressão de nêutrons degenerados e da pressão devida à ação repulsiva da interação forte entre bárions.
Estas restrições nos estados quânticos fazem com que as partículas adquiram momentos muito elevados, já que não têm outras posições do espaço de fases onde situar-se; pode-se dizer que o gás, ao não poder ocupar mais posições, se vê obrigado a estender-se no espaço de momentos com a limitação da velocidade c (velocidade da luz). Assim, ao estar tão comprimida a matéria, os estados energeticamente baixos preenchem-se em seguida, pelo que muitas partículas não têm outra possibilidade senão colocar-se em estados muito energéticos, o que envolve uma pressão adicional de origem quântica. Se a matéria está suficientemente degenerada, esta citada pressão será dominante, e muito, sobre todas as demais contribuições. Esta pressão é, além disto, independente da temperatura e unicamente dependente da densidade.
Estas características implicam tratamento termodinâmico bastante diverso e adequado às pressões e campos gravitacionais envolvidos[5], assim como o comportamento das reações nucleares na proximidade de tais massas.[6][7]
Necessita-se de densidades para chegar aos estados de degeneração da matéria. Para a degeneração de elétrons se requer uma densidade em torno dos 106 g/cm³, para a de nêutrons necessita-se muito mais ainda, 1014 g/cm³.
- A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:onde εF é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, εF/k. Esta temperatura característica é da ordem de 105K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.
- A flexoeletricidade é uma propriedade de um material dielétrico, pelo qual exibe uma polarização elétrica espontânea induzida por um gradiente de deformação.[1] A flexoeletricidade está intimamente relacionada à piezoeletricidade, mas enquanto a piezoeletricidade se refere à polarização devido à tensão uniforme, a flexoeletricidade se refere especificamente à polarização devido à tensão que muda de um ponto para outro no material.[2] Flexoeletricidade não é o mesmo que Ferroelasticidade[3].A polarização elétrica devido ao estresse mecânico em um dielétrico é dada por:onde o primeiro termo corresponde ao efeito piezoelétrico direto e o segundo termo corresponde à polarização flexoelétrica induzida pelo gradiente de deformação.Aqui, o coeficiente flexoelétrico, , é um tensor polar de quarta ordem e é o coeficiente correspondente ao efeito piezoelétrico direto.
- Denomina-se matéria degenerada, ou ainda gás degenerado, aquela na qual uma fração importante da pressão provém do princípio de exclusão de Pauli, que estabelece que dois férmions não podem ter os mesmos números quânticos.Tal "gás" não obedece às leis clássicas segundo as quais a pressão de um gás é proporcional à sua temperatura e densidade.Enrico Fermi e Paul Adrien Maurice Dirac provaram que, a uma densidade muito alta, a pressão aumenta rapidamente até o ponto em que ela passa a independer da temperatura do gás. Neste ponto, o gás passa a agir quase como um sólido.Na astronomia, este gás é encontrado nas estrelas anãs brancas e é importante no tratamento tanto de estrelas residuais densas quanto das novas que as geram.[1] É conceito importante em cosmologia e na evolução do universo no tempo,[2] com relações com a teoria da relatividade[3] e para o modelo "big bang" e na detecção de objetos estelares.[4]Dependendo das condições, a degeneração de diferentes partículas pode contribuir com a pressão de um objeto compacto, de modo que uma anã branca está sustentada pela degeneração dos elétrons, ainda que uma estrela de nêutrons não colapse devido ao efeito combinado da pressão de nêutrons degenerados e da pressão devida à ação repulsiva da interação forte entre bárions.Estas restrições nos estados quânticos fazem com que as partículas adquiram momentos muito elevados, já que não têm outras posições do espaço de fases onde situar-se; pode-se dizer que o gás, ao não poder ocupar mais posições, se vê obrigado a estender-se no espaço de momentos com a limitação da velocidade c (velocidade da luz). Assim, ao estar tão comprimida a matéria, os estados energeticamente baixos preenchem-se em seguida, pelo que muitas partículas não têm outra possibilidade senão colocar-se em estados muito energéticos, o que envolve uma pressão adicional de origem quântica. Se a matéria está suficientemente degenerada, esta citada pressão será dominante, e muito, sobre todas as demais contribuições. Esta pressão é, além disto, independente da temperatura e unicamente dependente da densidade.Estas características implicam tratamento termodinâmico bastante diverso e adequado às pressões e campos gravitacionais envolvidos[5], assim como o comportamento das reações nucleares na proximidade de tais massas.[6][7]Necessita-se de densidades para chegar aos estados de degeneração da matéria. Para a degeneração de elétrons se requer uma densidade em torno dos 106 g/cm³, para a de nêutrons necessita-se muito mais ainda, 1014 g/cm³.
Índice
Tratamento matemático da degeneração[editar | editar código-fonte]
-
Para calcular o número de partículas fermiônicas em função de seu momento, se usará a distribuição de Fermi-Dirac (ver estatística de Fermi-Dirac) da seguinte maneira:
Onde n(p) é o número de partículas com momento linear p. O coeficiente inicial 2 é a dupla degeneração de spin dos férmions. A primeira fração é o volume do espaço de fases em um diferencial de momentos dividido pelo volume de uma determinada seção no espaço. A h³ é a constante de Planck ao cubo que, como se tem dito, significa o volume dessas seções nas quais cabem até duas partículas com spins opostos. O último termo fracionário é o denominado fator de preenchimento. K é a constante de Boltzmann, T a temperatura, Ep a energia cinética de uma partícula com momento p e ψ o parâmetro de degeneração, que é dependente da densidade e da temperatura.
- O fator de preenchimento indica a probabilidade de este preencher um estado. Seu valor está compreendido entre 0 (todos vazios) e 1 (todos preenchidos).
- O parâmetro de degeneração indica o grau de degeneração das partículas. Se toma valores grandes e negativos a matéria estará em um regime de gás ideal. Se está próximo a 0 a degeneração se começa a notar. Diz-se que o material está parcialmente degenerado. Se o valor é grande e positivo o material está altamente degenerado. Isto acontece quando as densidades são elevadas ou também quando as temperaturas são baixas.
Desta equação se podem deduzir as integrais do número de partículas, a pressão que exercem e a energia que têm. Estas integrais são possíveis de serem resolvidas analiticamente quando a degeneração é completa.
O valor da energia das partículas dependerá da velocidade das partículas, a qual decidirá se se tem-se um gás relativista ou não. No primeiro caso se usarão as equações de Einstein e no segundo valerá a aproximação clássica. Como se pode ver, as relações energia-pressão variam significativamente, sendo maiores as pressões obtidas com a degeneração completa não relativista. É lógico, já que a matéria relativista é mais quente.
- Matéria degenerada não relativista (NR):
- Matéria degenerada extremamente relativista (ER):
As estrelas típicas com degeneração são as anãs brancas e as anãs marrons sustentadas por elétrons e as estrelas de nêutrons sustentadas por nêutrons degenerados. Considera-se que sua temperatura tende a 0, já que não possuem fonte de calor alguma. Suporemos estes corpos com um parâmetro de degeneração tendente a +infinito.
-
-
-
-
-
-
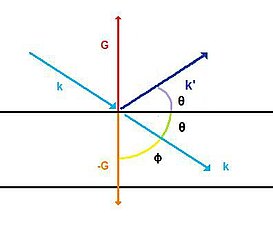
Em física do estado sólido, a Lei de Bragg está relacionada ao espalhamento de ondas que incidem em um cristal e fornece uma explicação para os efeitos difrativos observados nesta interação. Estes padrões são explicados relacionando os vetores de onda do feixe incidente e espalhado em uma rede cristalina para o caso de seu espalhamento elástico com os átomos do material.
No caso de ondas de raios X, ao atingirem um átomo, o campo elétrico da radiação provoca uma força na nuvem eletrônica acelerando as cargas livres do material (elétrons). O movimento dessas cargas re-irradia ondas que têm aproximadamente a mesma frequência, uma vez que o espalhamento não é totalmente elástico, podendo haver interações de criação e aniquilação de fônons, porém em uma escala de energia muito menor. Nesse modelo, as frequências da radiação incidente e espalhada são consideradas idênticas. As ondas emergentes interferem entre si construtiva e destrutivamente, gerando padrões de difração no espaço que podem ser medidos em um filme ou detector. O padrão de difração resultante é a base da análise difrativa, chamada difração de Bragg.
- Para calcular o número de partículas fermiônicas em função de seu momento, se usará a distribuição de Fermi-Dirac (ver estatística de Fermi-Dirac) da seguinte maneira:Onde n(p) é o número de partículas com momento linear p. O coeficiente inicial 2 é a dupla degeneração de spin dos férmions. A primeira fração é o volume do espaço de fases em um diferencial de momentos dividido pelo volume de uma determinada seção no espaço. A h³ é a constante de Planck ao cubo que, como se tem dito, significa o volume dessas seções nas quais cabem até duas partículas com spins opostos. O último termo fracionário é o denominado fator de preenchimento. K é a constante de Boltzmann, T a temperatura, Ep a energia cinética de uma partícula com momento p e ψ o parâmetro de degeneração, que é dependente da densidade e da temperatura.
- O fator de preenchimento indica a probabilidade de este preencher um estado. Seu valor está compreendido entre 0 (todos vazios) e 1 (todos preenchidos).
- O parâmetro de degeneração indica o grau de degeneração das partículas. Se toma valores grandes e negativos a matéria estará em um regime de gás ideal. Se está próximo a 0 a degeneração se começa a notar. Diz-se que o material está parcialmente degenerado. Se o valor é grande e positivo o material está altamente degenerado. Isto acontece quando as densidades são elevadas ou também quando as temperaturas são baixas.
Desta equação se podem deduzir as integrais do número de partículas, a pressão que exercem e a energia que têm. Estas integrais são possíveis de serem resolvidas analiticamente quando a degeneração é completa.O valor da energia das partículas dependerá da velocidade das partículas, a qual decidirá se se tem-se um gás relativista ou não. No primeiro caso se usarão as equações de Einstein e no segundo valerá a aproximação clássica. Como se pode ver, as relações energia-pressão variam significativamente, sendo maiores as pressões obtidas com a degeneração completa não relativista. É lógico, já que a matéria relativista é mais quente.- Matéria degenerada não relativista (NR):
- Matéria degenerada extremamente relativista (ER):
As estrelas típicas com degeneração são as anãs brancas e as anãs marrons sustentadas por elétrons e as estrelas de nêutrons sustentadas por nêutrons degenerados. Considera-se que sua temperatura tende a 0, já que não possuem fonte de calor alguma. Suporemos estes corpos com um parâmetro de degeneração tendente a +infinito. - Em física do estado sólido, a Lei de Bragg está relacionada ao espalhamento de ondas que incidem em um cristal e fornece uma explicação para os efeitos difrativos observados nesta interação. Estes padrões são explicados relacionando os vetores de onda do feixe incidente e espalhado em uma rede cristalina para o caso de seu espalhamento elástico com os átomos do material.No caso de ondas de raios X, ao atingirem um átomo, o campo elétrico da radiação provoca uma força na nuvem eletrônica acelerando as cargas livres do material (elétrons). O movimento dessas cargas re-irradia ondas que têm aproximadamente a mesma frequência, uma vez que o espalhamento não é totalmente elástico, podendo haver interações de criação e aniquilação de fônons, porém em uma escala de energia muito menor. Nesse modelo, as frequências da radiação incidente e espalhada são consideradas idênticas. As ondas emergentes interferem entre si construtiva e destrutivamente, gerando padrões de difração no espaço que podem ser medidos em um filme ou detector. O padrão de difração resultante é a base da análise difrativa, chamada difração de Bragg.
Índice
História[editar | editar código-fonte]
-
A difração de Bragg (também chamada de formulação de Bragg da difração de raios X) foi proposta originalmente por William Lawrence Bragg e William Henry Bragg em 1913, em resposta à descoberta de que sólidos cristalinos produziam padrões intrigantes de reflexão de raios x (ao contrário, por exemplo, de um líquido). Eles descobriram que esses cristais, para alguns comprimentos de onda e ângulos de incidência específicos, produziam intensos picos de radiação refletida (conhecidos como picos de Bragg). O conceito de difração de Bragg se aplica igualmente a processos de difração de nêutrons e de elétrons[1]. Tanto os nêutrons quanto os raios X possuem comprimento de onda compatível com as distâncias interatômicas - da ordem de 150 pm - e, portanto, constituem uma excelente ferramenta para se explorar dimensões com essa ordem de grandeza.
W.L. Bragg explicou esse resultado empírico modelando o cristal como um conjunto de planos discretos, paralelos e separados por uma distância constante d, propondo que a radiação incidente produziria um pico de Bragg se as reflexões especulares de vários planos interferissem construtivamente, ou seja, se a diferença de fase entre as frentes de onda refletidas por planos consecutivos fosse de radianos.
A lei de Bragg foi derivada pelo físico Sir William Lawrence Bragg.[2] em 1912 e apresentada pela primeira vez em 11 de novembro desse mesmo ano à Sociedade Filosófica de Cambridge. Embora simples, a lei de Bragg confirmou a existência de partículas reais na escala atômica, e forneceu uma nova e poderosa ferramenta para o estudo de cristais utilizando difração de raios X e nêutrons. William Lawrence Bragg e seu pai, Sir William Henry Bragg, foram laureados com o Prêmio Nobel de física em 1915 por seu trabalho em determinar estruturas cristalinas, a começar pelo cloreto de sódio, o sulfeto de zinco e o diamante. Eles são a única equipe formada por pai e filho a ganhar o prêmio conjuntamente. W.L. Bragg tinha 25 anos de idade, o que faz dele o mais jovem laureado pela Academia Real das Ciências da Suécia.
- A difração de Bragg (também chamada de formulação de Bragg da difração de raios X) foi proposta originalmente por William Lawrence Bragg e William Henry Bragg em 1913, em resposta à descoberta de que sólidos cristalinos produziam padrões intrigantes de reflexão de raios x (ao contrário, por exemplo, de um líquido). Eles descobriram que esses cristais, para alguns comprimentos de onda e ângulos de incidência específicos, produziam intensos picos de radiação refletida (conhecidos como picos de Bragg). O conceito de difração de Bragg se aplica igualmente a processos de difração de nêutrons e de elétrons[1]. Tanto os nêutrons quanto os raios X possuem comprimento de onda compatível com as distâncias interatômicas - da ordem de 150 pm - e, portanto, constituem uma excelente ferramenta para se explorar dimensões com essa ordem de grandeza.W.L. Bragg explicou esse resultado empírico modelando o cristal como um conjunto de planos discretos, paralelos e separados por uma distância constante d, propondo que a radiação incidente produziria um pico de Bragg se as reflexões especulares de vários planos interferissem construtivamente, ou seja, se a diferença de fase entre as frentes de onda refletidas por planos consecutivos fosse de radianos.A lei de Bragg foi derivada pelo físico Sir William Lawrence Bragg.[2] em 1912 e apresentada pela primeira vez em 11 de novembro desse mesmo ano à Sociedade Filosófica de Cambridge. Embora simples, a lei de Bragg confirmou a existência de partículas reais na escala atômica, e forneceu uma nova e poderosa ferramenta para o estudo de cristais utilizando difração de raios X e nêutrons. William Lawrence Bragg e seu pai, Sir William Henry Bragg, foram laureados com o Prêmio Nobel de física em 1915 por seu trabalho em determinar estruturas cristalinas, a começar pelo cloreto de sódio, o sulfeto de zinco e o diamante. Eles são a única equipe formada por pai e filho a ganhar o prêmio conjuntamente. W.L. Bragg tinha 25 anos de idade, o que faz dele o mais jovem laureado pela Academia Real das Ciências da Suécia.
Condição de Bragg[editar | editar código-fonte]
-
A periodicidade do cristal faz com que haja planos de átomos separados por uma distância fixa nas diferentes direções do espaço. A difração de Bragg ocorre quando a radiação eletromagnética ou ondas de matéria de comprimento de onda comparável à distância entre dois planos de átomos é refletida especularmente por planos consecutivos.
Nota-se que partículas em movimento, incluindo elétrons, prótons e nêutrons têm um comprimento de onda associado de de Broglie dado por:
.
Nessa expressão, é o momento linear da partícula.
A próxima equação é conhecida como Lei de Bragg. Para que haja uma diferença de fase entre dois raios igual a radianos, é necessária a condição
onde é um número natural, é o comprimento de onda da radiação incidente, é a distância entre planos atômicos e é o ângulo de incidência em relação ao plano considerado. Dessa maneira, existe uma dependência entre o ângulo de incidência e a intensidade da onda refletida. Como cada plano reflete de a do total da radiação incidente, há de a planos contribuindo para a reflexão total. Se os raios refletidos estão fora de fase, a soma das muitas contribuições (reflexões por planos diferentes) tenderá a zero, de maneira que podem ser observados picos localizados nos ângulos em que a condição de Bragg é satisfeita[3].
- A periodicidade do cristal faz com que haja planos de átomos separados por uma distância fixa nas diferentes direções do espaço. A difração de Bragg ocorre quando a radiação eletromagnética ou ondas de matéria de comprimento de onda comparável à distância entre dois planos de átomos é refletida especularmente por planos consecutivos.Nota-se que partículas em movimento, incluindo elétrons, prótons e nêutrons têm um comprimento de onda associado de de Broglie dado por:.Nessa expressão, é o momento linear da partícula.A próxima equação é conhecida como Lei de Bragg. Para que haja uma diferença de fase entre dois raios igual a radianos, é necessária a condiçãoonde é um número natural, é o comprimento de onda da radiação incidente, é a distância entre planos atômicos e é o ângulo de incidência em relação ao plano considerado. Dessa maneira, existe uma dependência entre o ângulo de incidência e a intensidade da onda refletida. Como cada plano reflete de a do total da radiação incidente, há de a planos contribuindo para a reflexão total. Se os raios refletidos estão fora de fase, a soma das muitas contribuições (reflexões por planos diferentes) tenderá a zero, de maneira que podem ser observados picos localizados nos ângulos em que a condição de Bragg é satisfeita[3].
Densidade eletrônica[editar | editar código-fonte]
Análise de Fourier[editar | editar código-fonte]
-
Para melhor compreender o comportamento da onda espalhada, pode ser tomado como modelo um cristal perfeito, formado por uma célula primitiva que se repete no espaço. A descrição matemática do cristal é invariante sob uma translação espacial:
.
Nessa expressão os são números inteiros e os vetores são os vetores associados aos eixos do cristal, cujas magnitudes são as distâncias entre sítios (pontuais) da rede nas direções . Todas as propriedades locais do cristal, como densidade de momento magnético, concentração de carga ou densidade eletrônica, serão invariantes sob uma translação da forma para qualquer combinação de [4]
.
Essa periodicidade permite que se faça uma expansão da densidade eletrônica em série de Fourier. Considerando primeiro apenas uma componente dimensional, vem:
.
.
Um ponto é um ponto no chamado espaço recíproco do cristal. Os coeficientes da expansão serão tais que apenas os termos que condizem com a periodicidade do cristal no espaço real (das posições) poderão ser diferentes de zero.
É conveniente escrever a soma como uma exponencial complexa através da relação de Euler:
Com essa notação, a expansão pode ser escrita como
.
Nessa expressão o somatório percorre todos os valores inteiros de p. O termo agora é, em geral, um número complexo e, portanto, é necessário impor uma condição que faça com que seja uma função real como originalmente. A condição
faz com que
,
que é uma função real.
Estender o argumento para três dimensões é algo direto:
.
O somatório triplo foi omitido para preservar a clareza da expressão, mas é importante lembrar que a soma é realizada sobre todos as combinações possíveis de (definido na próxima subseção). Assim, é necessário encontrar um conjunto de vetores que satisfaçam a relação de invariância por translação .
Tendo a expressão para a expansão de Fourier para densidade eletrônica, é possível obter os coeficientes da expansão em uma dimensão por meio de
.
Substituindo a expressão expandida para na integral acima, vem:
.
O caso faz com que o valor da integral seja
,
pois é um inteiro e . No caso , , de maneira que o valor da integral é e . De maneira semelhante, pode ser invertido o caso tridimensional, obtendo
.
Nesse caso a integração é realizada sobre uma célula primitiva e é o volume da mesma.
- Para melhor compreender o comportamento da onda espalhada, pode ser tomado como modelo um cristal perfeito, formado por uma célula primitiva que se repete no espaço. A descrição matemática do cristal é invariante sob uma translação espacial:.Nessa expressão os são números inteiros e os vetores são os vetores associados aos eixos do cristal, cujas magnitudes são as distâncias entre sítios (pontuais) da rede nas direções . Todas as propriedades locais do cristal, como densidade de momento magnético, concentração de carga ou densidade eletrônica, serão invariantes sob uma translação da forma para qualquer combinação de [4].Essa periodicidade permite que se faça uma expansão da densidade eletrônica em série de Fourier. Considerando primeiro apenas uma componente dimensional, vem:..Um ponto é um ponto no chamado espaço recíproco do cristal. Os coeficientes da expansão serão tais que apenas os termos que condizem com a periodicidade do cristal no espaço real (das posições) poderão ser diferentes de zero.É conveniente escrever a soma como uma exponencial complexa através da relação de Euler:Com essa notação, a expansão pode ser escrita como.Nessa expressão o somatório percorre todos os valores inteiros de p. O termo agora é, em geral, um número complexo e, portanto, é necessário impor uma condição que faça com que seja uma função real como originalmente. A condiçãofaz com que,que é uma função real.Estender o argumento para três dimensões é algo direto:.O somatório triplo foi omitido para preservar a clareza da expressão, mas é importante lembrar que a soma é realizada sobre todos as combinações possíveis de (definido na próxima subseção). Assim, é necessário encontrar um conjunto de vetores que satisfaçam a relação de invariância por translação .Tendo a expressão para a expansão de Fourier para densidade eletrônica, é possível obter os coeficientes da expansão em uma dimensão por meio de.Substituindo a expressão expandida para na integral acima, vem:.O caso faz com que o valor da integral seja,pois é um inteiro e . No caso , , de maneira que o valor da integral é e . De maneira semelhante, pode ser invertido o caso tridimensional, obtendo.Nesse caso a integração é realizada sobre uma célula primitiva e é o volume da mesma.
Rede recíproca[editar | editar código-fonte]
-
ou de forma condensada, utilizando o tensor ou símbolo de Levi-Civita,
Por análise vetorial simples temos
onde é o delta de Kronecker.
Definimos como sendo um vetor da forma
,
onde os são números inteiros e os são a base da rede recíproca. Estamos agora em condições de descrever a periodicidade de combinando a definição de e a expansão em coeficientes de Fourier de :
O termo à direita pode ser escrito como
e como todos os são inteiros e a exponencial de vezes um número inteiro é um, obtemos o resultado desejado, isto é, a invariância da densidade eletrônica, pois
.
-
ou de forma condensada, utilizando o tensor ou símbolo de Levi-Civita,Por análise vetorial simples temosonde é o delta de Kronecker.Definimos como sendo um vetor da forma,onde os são números inteiros e os são a base da rede recíproca. Estamos agora em condições de descrever a periodicidade de combinando a definição de e a expansão em coeficientes de Fourier de :O termo à direita pode ser escrito comoe como todos os são inteiros e a exponencial de vezes um número inteiro é um, obtemos o resultado desejado, isto é, a invariância da densidade eletrônica, pois.
Amplitude de Espalhamento[editar | editar código-fonte]
-
Definimos a amplitude de espalhamento como sendo uma função que depende da densidade eletrônica e dos vetores de ondas incidente e refletido e , a princípio ondas planas monocromáticas:
.
As integrais são realizadas sobre o volume do cristal inteiro. Embora tenhamos considerado um modelo onde o cristal é perfeito e infinito, uma amostra macroscópica é aproximadamente infinita se comparadas as suas dimensões com as distâncias interatômicas de uma rede cristalina, da ordem de metros[6]. O vetor de onda incidente tem a mesma energia que o vetor difratado, conforme a condição de espalhamento elástico considerando a rede cristalina como muito massiva e imóvel. A condição de conservação de energia é
.
Definimos o vetor de espalhamento como sendo
,
de maneira que a expressão anterior se torna
.
Introduzimos agora a expansão em série de Fourier para nessa expressão para obter
.
Quando o vetor de espalhamento é igual a algum vetor da rede recíproca, isto é,
,
a exponencial é nula e
.
Quando o vetor de espalhamento difere significantemente de qualquer vetor da rede recíproca, o grande número de oscilações da exponencial devido à variação de dentro da integral faz com que rapidamente tenda a zero.
Podemos reescrever a relação entre os vetores de onda e os vetores da base recíproca utilizando a definição do vetor de espalhamento
.
Pela conservação da energia, obtivemos que as magnitudes dos vetores devem ser iguais. Portanto, tomando o produto escalar dos dois lados:
Portanto,
.
ou ainda
.
Pelas definições de rede recíproca, é possível mostrar que, se é um vetor da rede recíproca, então também é. Isso faz com que seja possível escrever a condição acima como
.
As últimas duas equações são formulações equivalentes da condição de difração de Bragg. O espaçamento entre planos cristalinos paralelos entre si, normais à direção
,
onde h, k, l são inteiros, é dado por
.
Combinando a definição de ,
onde é o comprimento de onda incidente, com a definição de produto escalar e do módulo de , temos:
,
sendo o ângulo entre os vetores e .
Conforme observamos acima, o vetor é normal ao plano . Logo, o vetor também é normal ao plano e o ângulo entre esse vetor e um vetor no plano considerado é . O menor ângulo formado entre o vetor de onda incidente e o plano é, por análise geométrica, igual a
ou rearranjando os fatores:
.
Podemos reescrever a condição de Bragg utilizando o ângulo entre o vetor incidente e o plano, ao invés de considerar o ângulo entre o vetor incidente e o vetor , utilizando a relação
Assim, recuperamos o resultado obtido pela análise geométrica simples, escrito à maneira usual da formulação da lei de Bragg:
.
Aqui, é o ângulo entre o vetor de onda e o plano cristalino descrito pelos inteiros h, k e l. Existe uma diferença entre essa equação e a primeira equação apresentada aqui como condição de difração, a saber, a multiplicação do lado direito da equação por um número inteiro. Isso se dá pelo fato dos índices de Miller poderem conter um fator comum n, que é eliminado no processo de obtenção dos mesmos. Fisicamente, isso significa que a expressão
dá a condição de difração de Bragg para um plano de índices de Miller .
-
-
-
-
-
-
A lei de Wiedemann-Franz afirma que a contribuição eletrônica para a condutividade térmica e condutividade elétrica de um metal é proporcional a temperatura. Esta é uma lei empírica definida por Gustav Wiedemann e Rudolph Franz em 1853,
Somente em 1872 o físico dinamarquês Ludvig Lorenz determinou a constante de proporcionalidade . Essa constante é idêntica para todos os metais e é conhecida como número de Lorenz
A interligação entre a condutividade elétrica e a condutividade térmica é explicada pelo fato de que ambas as propriedades nos metais são consequência principal do movimento dos elétrons condutores. A lei Wiedemann-Franz foi explicada pela primeira vez pelo físico alemão P. Drude, que considerada em seu modelo que os elétrons do metal se comportavam como um gás de elétrons. No entanto, somente com o auxílio da mecânica quântica e da equação de Boltzmann, que a expressão exata para essa lei e o valor de foram obtidos, e estavam de comum acordo com os dados experimentais. Experimentos mostram que o valor de , apesar de aproximadamente constante, não tem o mesmo valor para todos os sólidos. Kittel [2] apresenta alguns valores de entre para o cobre a 0 °C e para o tungstênio a 100 °C. Rosenberg [3] observou que a lei Wiedemann-Franz geralmente é válida para altas e baixas temperaturas, mas não funciona bem para temperaturas intermediárias.
Número de Lorenz
Metal 273 K 373 K Ag 2.31 2.37 Au 2.35 2.40 Cd 2.42 2.43 Cu 2.23 2.33 Ir 2.49 2.49 Mo 2.61 2.79 Pb 2.47 2.56 Pt 2.51 2.60 Sn 2.52 2.49 W 3.04 3.20 Zn 2.31 2.33
-
O modelo de Drude para condução eléctrica foi desenvolvido até 1900 por Paul Drude para explicar as propriedades de transporte de elétrons em materiais (especialmente em metais). O modelo de Drude baseia-se na aplicação da teoria cinética aos electrões num sólido. Supõe que o material contém ions positivos imóveis e um "gás de elétrons" clássicos, que não interagem entre si, de densidade n, donde o movimento de cada um se encontra amortecido por uma força de fricção produto das colisões dos electrões com os iões, caracterizada por um tempo de relaxamento τ.
- Definimos a amplitude de espalhamento como sendo uma função que depende da densidade eletrônica e dos vetores de ondas incidente e refletido e , a princípio ondas planas monocromáticas:.As integrais são realizadas sobre o volume do cristal inteiro. Embora tenhamos considerado um modelo onde o cristal é perfeito e infinito, uma amostra macroscópica é aproximadamente infinita se comparadas as suas dimensões com as distâncias interatômicas de uma rede cristalina, da ordem de metros[6]. O vetor de onda incidente tem a mesma energia que o vetor difratado, conforme a condição de espalhamento elástico considerando a rede cristalina como muito massiva e imóvel. A condição de conservação de energia é.Definimos o vetor de espalhamento como sendo,de maneira que a expressão anterior se torna.Introduzimos agora a expansão em série de Fourier para nessa expressão para obter.Quando o vetor de espalhamento é igual a algum vetor da rede recíproca, isto é,,a exponencial é nula e.Quando o vetor de espalhamento difere significantemente de qualquer vetor da rede recíproca, o grande número de oscilações da exponencial devido à variação de dentro da integral faz com que rapidamente tenda a zero.Podemos reescrever a relação entre os vetores de onda e os vetores da base recíproca utilizando a definição do vetor de espalhamento.Pela conservação da energia, obtivemos que as magnitudes dos vetores devem ser iguais. Portanto, tomando o produto escalar dos dois lados:Portanto,.ou ainda.Pelas definições de rede recíproca, é possível mostrar que, se é um vetor da rede recíproca, então também é. Isso faz com que seja possível escrever a condição acima como.As últimas duas equações são formulações equivalentes da condição de difração de Bragg. O espaçamento entre planos cristalinos paralelos entre si, normais à direção,onde h, k, l são inteiros, é dado por.Combinando a definição de ,onde é o comprimento de onda incidente, com a definição de produto escalar e do módulo de , temos:,sendo o ângulo entre os vetores e .Conforme observamos acima, o vetor é normal ao plano . Logo, o vetor também é normal ao plano e o ângulo entre esse vetor e um vetor no plano considerado é . O menor ângulo formado entre o vetor de onda incidente e o plano é, por análise geométrica, igual aou rearranjando os fatores:.Podemos reescrever a condição de Bragg utilizando o ângulo entre o vetor incidente e o plano, ao invés de considerar o ângulo entre o vetor incidente e o vetor , utilizando a relaçãoAssim, recuperamos o resultado obtido pela análise geométrica simples, escrito à maneira usual da formulação da lei de Bragg:.Aqui, é o ângulo entre o vetor de onda e o plano cristalino descrito pelos inteiros h, k e l. Existe uma diferença entre essa equação e a primeira equação apresentada aqui como condição de difração, a saber, a multiplicação do lado direito da equação por um número inteiro. Isso se dá pelo fato dos índices de Miller poderem conter um fator comum n, que é eliminado no processo de obtenção dos mesmos. Fisicamente, isso significa que a expressãodá a condição de difração de Bragg para um plano de índices de Miller .
- A lei de Wiedemann-Franz afirma que a contribuição eletrônica para a condutividade térmica e condutividade elétrica de um metal é proporcional a temperatura. Esta é uma lei empírica definida por Gustav Wiedemann e Rudolph Franz em 1853,Somente em 1872 o físico dinamarquês Ludvig Lorenz determinou a constante de proporcionalidade . Essa constante é idêntica para todos os metais e é conhecida como número de LorenzA interligação entre a condutividade elétrica e a condutividade térmica é explicada pelo fato de que ambas as propriedades nos metais são consequência principal do movimento dos elétrons condutores. A lei Wiedemann-Franz foi explicada pela primeira vez pelo físico alemão P. Drude, que considerada em seu modelo que os elétrons do metal se comportavam como um gás de elétrons. No entanto, somente com o auxílio da mecânica quântica e da equação de Boltzmann, que a expressão exata para essa lei e o valor de foram obtidos, e estavam de comum acordo com os dados experimentais. Experimentos mostram que o valor de , apesar de aproximadamente constante, não tem o mesmo valor para todos os sólidos. Kittel [2] apresenta alguns valores de entre para o cobre a 0 °C e para o tungstênio a 100 °C. Rosenberg [3] observou que a lei Wiedemann-Franz geralmente é válida para altas e baixas temperaturas, mas não funciona bem para temperaturas intermediárias.
Número de Lorenz Metal 273 K 373 K Ag 2.31 2.37 Au 2.35 2.40 Cd 2.42 2.43 Cu 2.23 2.33 Ir 2.49 2.49 Mo 2.61 2.79 Pb 2.47 2.56 Pt 2.51 2.60 Sn 2.52 2.49 W 3.04 3.20 Zn 2.31 2.33 - O modelo de Drude para condução eléctrica foi desenvolvido até 1900 por Paul Drude para explicar as propriedades de transporte de elétrons em materiais (especialmente em metais). O modelo de Drude baseia-se na aplicação da teoria cinética aos electrões num sólido. Supõe que o material contém ions positivos imóveis e um "gás de elétrons" clássicos, que não interagem entre si, de densidade n, donde o movimento de cada um se encontra amortecido por uma força de fricção produto das colisões dos electrões com os iões, caracterizada por um tempo de relaxamento τ.
Explicação[editar | editar código-fonte]
-
O modelo de Drude supõe que um portador médio de carga eléctrica está sujeito à acção de uma `força de resistência' . Em presença de um campo eléctrico externo E satisfaz-se a seguinte equação diferencial:
onde é a velocidade média, m é a massa efectiva e q a carga eléctrica do portador de carga.
A solução estacionária () desta equação diferencial é:
onde:
é o tempo livre médio de um portador de carga, e é a mobilidade eléctrica. Se se introduz a densidade do gás de portadores de carga n (partículas por unidade de volume), podemos relacionar a velocidade média com uma corrente eléctrica:
Pode-se demonstrar que o material satisfaz a lei de Ohm com uma condutividade eléctrica em corrente eléctrica continua .
O modelo de Drude permite também predizer a corrente como uma resposta a um campo eléctrico variável no tempo com uma frequência angular , em cujo caso:
Onde se supõe que:
Em outras convenções, \, i é substituido por \, -i em todas as equações. A parte imaginária indica que a corrente está atrasada com respeito ao campo eléctrico, o que se produz porque os electrões necessitam aproximadamente um tempo para acelerarem-se em resposta a uma mudança eo campo eléctrico aplicado. No caso prévio o modelo de Drude aplicou-se aos electrões; mas também pode ser aplicado a buracos, quer dizer, aos portadores de carga positiva nos semiconductores.
-
-
-
-
-
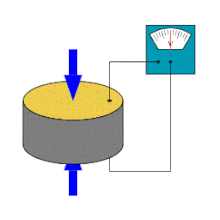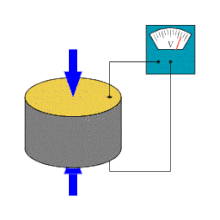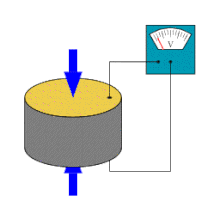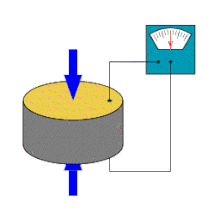
Piezoeletricidade é a capacidade de alguns cristais gerarem tensão elétrica por resposta a uma pressão mecânica. O termo piezoeletricidade provém do grego piezein, que significa apertar/pressionar. Referente à geração de corrente elétrica, juntou-se a designação eletricidade, de modo que piezoeletricidade é interpretado como a produção de energia elétrica devido à compressão sobre determinados materiais.
- O modelo de Drude supõe que um portador médio de carga eléctrica está sujeito à acção de uma `força de resistência' . Em presença de um campo eléctrico externo E satisfaz-se a seguinte equação diferencial:onde é a velocidade média, m é a massa efectiva e q a carga eléctrica do portador de carga.A solução estacionária () desta equação diferencial é:onde:é o tempo livre médio de um portador de carga, e é a mobilidade eléctrica. Se se introduz a densidade do gás de portadores de carga n (partículas por unidade de volume), podemos relacionar a velocidade média com uma corrente eléctrica:Pode-se demonstrar que o material satisfaz a lei de Ohm com uma condutividade eléctrica em corrente eléctrica continua .O modelo de Drude permite também predizer a corrente como uma resposta a um campo eléctrico variável no tempo com uma frequência angular , em cujo caso:Onde se supõe que:Em outras convenções, \, i é substituido por \, -i em todas as equações. A parte imaginária indica que a corrente está atrasada com respeito ao campo eléctrico, o que se produz porque os electrões necessitam aproximadamente um tempo para acelerarem-se em resposta a uma mudança eo campo eléctrico aplicado. No caso prévio o modelo de Drude aplicou-se aos electrões; mas também pode ser aplicado a buracos, quer dizer, aos portadores de carga positiva nos semiconductores.
- Piezoeletricidade é a capacidade de alguns cristais gerarem tensão elétrica por resposta a uma pressão mecânica. O termo piezoeletricidade provém do grego piezein, que significa apertar/pressionar. Referente à geração de corrente elétrica, juntou-se a designação eletricidade, de modo que piezoeletricidade é interpretado como a produção de energia elétrica devido à compressão sobre determinados materiais.
Índice
Mecanismo[editar | editar código-fonte]
-
O efeito piezoelétrico é entendido como a interação eletromecânica linear entre a força mecânica e o estado elétrico (forças de Coulomb) em materiais cristalinos (cerâmicos, polímeros).
O efeito piezoelétrico é um processo reversível em que os materiais exibem o efeito piezoelétrico direto (a geração interna de carga elétrica resultante de uma força mecânica aplicada), mas também exibem o efeito piezoelétrico reverso (a geração interna de uma tensão mecânica resultante de um campo elétrico aplicado). Por exemplo, os cristais de titanato zirconato de chumbo irão gerar piezoeletricidade mensurável quando a sua estrutura estática é deformada por cerca de 0,1% da dimensão inicial. Por outro lado, esses mesmos cristais mudam cerca de 0,1% da sua dimensão estática quando um campo elétrico externo é aplicado ao material. Como exemplo, o efeito piezoelétrico inverso é usado na produção de ondas de ultrassom.[1]
- O efeito piezoelétrico é entendido como a interação eletromecânica linear entre a força mecânica e o estado elétrico (forças de Coulomb) em materiais cristalinos (cerâmicos, polímeros).O efeito piezoelétrico é um processo reversível em que os materiais exibem o efeito piezoelétrico direto (a geração interna de carga elétrica resultante de uma força mecânica aplicada), mas também exibem o efeito piezoelétrico reverso (a geração interna de uma tensão mecânica resultante de um campo elétrico aplicado). Por exemplo, os cristais de titanato zirconato de chumbo irão gerar piezoeletricidade mensurável quando a sua estrutura estática é deformada por cerca de 0,1% da dimensão inicial. Por outro lado, esses mesmos cristais mudam cerca de 0,1% da sua dimensão estática quando um campo elétrico externo é aplicado ao material. Como exemplo, o efeito piezoelétrico inverso é usado na produção de ondas de ultrassom.[1]
Cristais[editar | editar código-fonte]
-
Utilizando argumentos referentes à simetria, o efeito piezoelétrico não existe em materiais que apresentam simetria central, e desta forma, podem ser polarizados, ou seja, a piezoeletricidade pode ser explicada pela assimetria de polarização iônica. Porém, elementos puros, tais como selênio (Se) e telúrio (Te) também exibem a propriedade de piezoeletricidade. Nestes casos, a polarização elétrica induzida é atribuída à distribuição eletrônica, que é alterada pela ação externa.
Considerando as trinta e duas classes de cristais catalogadas, 21 não são centrossimétricas (não possuem centro de simetria); vinte destes exibem piezoeletricidade direta; dez destes representam as classes de cristal polares, que mostram uma polarização espontânea, sem estresse mecânico devido a um momento de dipolo elétrico permanente. Se o momento de dipolo puder ser revertido por meio da aplicação de um campo elétrico externo, então o material é considerado ferroelétrico.
Para cristais polares, para os quais o momento de dipolo P diferente de zero se mantém sem se aplicar uma carga mecânica, o efeito piezoelétrico manifesta-se alterando a magnitude ou a direção do vetor momento de dipolo ou ambos. Para os cristais não-polares, mas piezoelétricos, a polarização diferente de zero é apenas induzida pela aplicação de uma carga mecânica. Para eles, a tensão pode ser imaginada para transformar o material a partir de uma classe de cristal não polar (P = 0) para uma polar, para a qual P ≠ 0.
A maioria dos cristais não possui propriedades piezoelétricas. O mais importante cristal natural que possui esta propriedade é o quartzo. Além deste, pela facilidade de sintetização, os cristais utilizados são cerâmicas à base de, por exemplo, titanato de bário ou zirconato de chumbo.[2]
- Utilizando argumentos referentes à simetria, o efeito piezoelétrico não existe em materiais que apresentam simetria central, e desta forma, podem ser polarizados, ou seja, a piezoeletricidade pode ser explicada pela assimetria de polarização iônica. Porém, elementos puros, tais como selênio (Se) e telúrio (Te) também exibem a propriedade de piezoeletricidade. Nestes casos, a polarização elétrica induzida é atribuída à distribuição eletrônica, que é alterada pela ação externa.Considerando as trinta e duas classes de cristais catalogadas, 21 não são centrossimétricas (não possuem centro de simetria); vinte destes exibem piezoeletricidade direta; dez destes representam as classes de cristal polares, que mostram uma polarização espontânea, sem estresse mecânico devido a um momento de dipolo elétrico permanente. Se o momento de dipolo puder ser revertido por meio da aplicação de um campo elétrico externo, então o material é considerado ferroelétrico.Para cristais polares, para os quais o momento de dipolo P diferente de zero se mantém sem se aplicar uma carga mecânica, o efeito piezoelétrico manifesta-se alterando a magnitude ou a direção do vetor momento de dipolo ou ambos. Para os cristais não-polares, mas piezoelétricos, a polarização diferente de zero é apenas induzida pela aplicação de uma carga mecânica. Para eles, a tensão pode ser imaginada para transformar o material a partir de uma classe de cristal não polar (P = 0) para uma polar, para a qual P ≠ 0.A maioria dos cristais não possui propriedades piezoelétricas. O mais importante cristal natural que possui esta propriedade é o quartzo. Além deste, pela facilidade de sintetização, os cristais utilizados são cerâmicas à base de, por exemplo, titanato de bário ou zirconato de chumbo.[2]
Descrição matemática[editar | editar código-fonte]
-
A piezoelectricidade é uma combinação de efeitos do comportamento elétrico do material:[3]
Nessa equação, D é o deslocamento elétrico, ε é a permissividade elétrica, E representa o campo elétrico, 'e' representa a constante de stress e S é a tensão longitudinal aplicada.
Quando a aplicação de uma força F, o centro de equilíbrio das cargas positivas e negativas é deslocado, causando a polarização do material, e o consequente deslocamento de corrente.
Similarmente, considerações para o caso quando um campo elétrico E é aplicado mostram que um termo referente a stress adicional, -eE, aparece. Tem-se então a Lei de Hooke, T = cS:
Se as cargas de moléculas positivas e negativas possuem magnitudes diferentes, há uma polarização espontânea. Se uma molécula possui um momento de dipolo, este material exibe uma polarização iônica. Já no caso onde há somente um tipo de elemento, mas este é polarizável, temos o efeito de polarização eletrônica.
A piezoeletricidade apresenta relação entre propriedades elétricas (E, D) e mecânicas (S, T). O modelo de um sólido piezoelétrico apresenta quatro diferentes relações entre variáveis. Assumimos que e . Assim, temos
onde todos os outros efeitos, tais como magnéticos e térmicos, assim como termos não-lineares, são ignorados.
Considerando o caso onde ao campo elétrico é aplicado sobre o material piezoelétrico (ao se colocar um material piezoelétrico num campo elétrico externo, as cargas elétricas da rede cristalina interagem com o mesmo e produzem tensões mecânicas), os segundos termos das equações acima enunciam o stress ou a tensão elétrica no material. Se o material não está confinado mecanicamente, a tensão será uma força de reação a força imposta pelo stress. Desta forma, a tensão altera a relação D e E, e assim a medição das propriedades elétricas dependentes das propriedades mecânicas. Do mesmo modo, uma tensão elétrica alterará a medição de propriedades mecânicas dependentes das propriedades elétricas. Em ambos os casos, isso demonstra a essência do acoplamento piezoelétrico. Para uma análise mais detalhada, deve-se comparar diferentes materiais piezoelétricos para identificar sua performance. Fatores como a eficiência do acoplamento a vibrações mecânicas, vibrações com campos elétricos externos, direção de aplicação do campo elétrico externo e demais, são resultados a serem considerados.
Num material piezoelétrico também interessam os seguintes coeficientes:
- Coeficiente de acoplamento eletro-mecânico:
é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.
- Coeficiente Dielétrica: esta grandeza relaciona a quantidade de carga que uma das faces do cristal pode armazenar em relação à carga total armazenada, e que pode ser dissipada como corrente real. Existem duas constantes dielétricas: uma é a constante para o cristal livre e outra para o cristal bloqueado:
-
-
-
-
A Superfície de Fermi é definida como a superfície de energia constante no espaço recíproco. Na temperatura do zero absoluto, a superfície de Fermi separa os orbitais vazios dos orbitais ocupados. Como a corrente elétrica se deve a mudanças na ocupação dos estados próximos da superfície de Fermi, a forma e volume desta determina as propriedades elétricas de um metal. Além disso, a superfície de Fermi também é útil para determinar propriedades térmicas, magnéticas e ópticas dos metais.
- A piezoelectricidade é uma combinação de efeitos do comportamento elétrico do material:[3]Nessa equação, D é o deslocamento elétrico, ε é a permissividade elétrica, E representa o campo elétrico, 'e' representa a constante de stress e S é a tensão longitudinal aplicada.Quando a aplicação de uma força F, o centro de equilíbrio das cargas positivas e negativas é deslocado, causando a polarização do material, e o consequente deslocamento de corrente.Similarmente, considerações para o caso quando um campo elétrico E é aplicado mostram que um termo referente a stress adicional, -eE, aparece. Tem-se então a Lei de Hooke, T = cS:Se as cargas de moléculas positivas e negativas possuem magnitudes diferentes, há uma polarização espontânea. Se uma molécula possui um momento de dipolo, este material exibe uma polarização iônica. Já no caso onde há somente um tipo de elemento, mas este é polarizável, temos o efeito de polarização eletrônica.A piezoeletricidade apresenta relação entre propriedades elétricas (E, D) e mecânicas (S, T). O modelo de um sólido piezoelétrico apresenta quatro diferentes relações entre variáveis. Assumimos que e . Assim, temosonde todos os outros efeitos, tais como magnéticos e térmicos, assim como termos não-lineares, são ignorados.Considerando o caso onde ao campo elétrico é aplicado sobre o material piezoelétrico (ao se colocar um material piezoelétrico num campo elétrico externo, as cargas elétricas da rede cristalina interagem com o mesmo e produzem tensões mecânicas), os segundos termos das equações acima enunciam o stress ou a tensão elétrica no material. Se o material não está confinado mecanicamente, a tensão será uma força de reação a força imposta pelo stress. Desta forma, a tensão altera a relação D e E, e assim a medição das propriedades elétricas dependentes das propriedades mecânicas. Do mesmo modo, uma tensão elétrica alterará a medição de propriedades mecânicas dependentes das propriedades elétricas. Em ambos os casos, isso demonstra a essência do acoplamento piezoelétrico. Para uma análise mais detalhada, deve-se comparar diferentes materiais piezoelétricos para identificar sua performance. Fatores como a eficiência do acoplamento a vibrações mecânicas, vibrações com campos elétricos externos, direção de aplicação do campo elétrico externo e demais, são resultados a serem considerados.Num material piezoelétrico também interessam os seguintes coeficientes:
- Coeficiente de acoplamento eletro-mecânico:
é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.- Coeficiente Dielétrica: esta grandeza relaciona a quantidade de carga que uma das faces do cristal pode armazenar em relação à carga total armazenada, e que pode ser dissipada como corrente real. Existem duas constantes dielétricas: uma é a constante para o cristal livre e outra para o cristal bloqueado:
- A Superfície de Fermi é definida como a superfície de energia constante no espaço recíproco. Na temperatura do zero absoluto, a superfície de Fermi separa os orbitais vazios dos orbitais ocupados. Como a corrente elétrica se deve a mudanças na ocupação dos estados próximos da superfície de Fermi, a forma e volume desta determina as propriedades elétricas de um metal. Além disso, a superfície de Fermi também é útil para determinar propriedades térmicas, magnéticas e ópticas dos metais.
Índice
Teoria[editar | editar código-fonte]
-
Muitas das propriedades de um material podem ser calculadas ignorando a dinâmica das interações dos elétrons entre si e com rede cristalina. Porém, existem aproximações de interações fracas entre elétrons e a rede, ou seja, assumindo que eles se movem em um potencial periódico fixo que é criado por uma rede perfeitamente rigida de íons e por uma distribuição média de elétrons.
Como estamos interessados em descrever apenas os elétrons exteriores, podemos incluir ao potencial efetivo um termo fortemente repulsivo representando o principio de exclusão de Pauli e o fato das funções de onda do núcleo e do estado de condução serem ortogonais entre si. Esse potencial é chamado de pseudopotencial e é aproximadamente zero, devido a soma do termo repulsivo e do termo atrativo, para a maior parte dos casos.
As soluções da equação de Schrodinger com um pseudopotencial fornecem o número de autoestados da partícula única, e variam continuamente com o vetor de onda k, assim elas podem ser expressas como uma sequência de funções continuas de k, , onde n é o número da n-ésima banda de energia.
Essas funções são periódicas no espaço recíproco, e para contar cada estado apenas uma vez, vamos nos restringir apenas à primeira zona de Brillouin. Na temperatura de zero absoluto, os elétrons em um sólido preenchem os estados de energia começando pelo estado mais baixo. O número total de elétrons determina quantas bandas disponíveis serão preenchidas com elétrons e se as últimas bandas serão preenchidas ou ficarão parcialmente vazias. Como estamos interessados em estudar os metais, vamos considerar apenas os casos onde as bandas são parcialmente preenchidas.
Se a n-ésima banda está parcialmente preenchida, os orbitais ocupados e os orbitais vazios da primeira zona de Brillouin são separados pela superfície de Fermi, que é definida como , onde a energia de Fermi, , é a mais alta energia para a qual existe um estado ocupado.
Um modelo simples para superfície de Fermi, o gás de elétrons livre, é obtido negligenciando os efeitos da não uniformidade do potencial sentido pelos elétrons na banda de condução. A energia de cada elétron é dada pela energia de partícula livre[1]:
onde estados de baixa energia preenchem uma esfera perfeita quando a temperatura é igual a zero; a superfície de Fermi é esférica. Para a maioria dos metais essa é uma ótima aproximação para a superfície de Fermi, especialmente pra metais monovalentes, onde a esfera de Fermi encontra-se totalmente na primeira zona de Brillouin.
- Muitas das propriedades de um material podem ser calculadas ignorando a dinâmica das interações dos elétrons entre si e com rede cristalina. Porém, existem aproximações de interações fracas entre elétrons e a rede, ou seja, assumindo que eles se movem em um potencial periódico fixo que é criado por uma rede perfeitamente rigida de íons e por uma distribuição média de elétrons.Como estamos interessados em descrever apenas os elétrons exteriores, podemos incluir ao potencial efetivo um termo fortemente repulsivo representando o principio de exclusão de Pauli e o fato das funções de onda do núcleo e do estado de condução serem ortogonais entre si. Esse potencial é chamado de pseudopotencial e é aproximadamente zero, devido a soma do termo repulsivo e do termo atrativo, para a maior parte dos casos.As soluções da equação de Schrodinger com um pseudopotencial fornecem o número de autoestados da partícula única, e variam continuamente com o vetor de onda k, assim elas podem ser expressas como uma sequência de funções continuas de k, , onde n é o número da n-ésima banda de energia.Essas funções são periódicas no espaço recíproco, e para contar cada estado apenas uma vez, vamos nos restringir apenas à primeira zona de Brillouin. Na temperatura de zero absoluto, os elétrons em um sólido preenchem os estados de energia começando pelo estado mais baixo. O número total de elétrons determina quantas bandas disponíveis serão preenchidas com elétrons e se as últimas bandas serão preenchidas ou ficarão parcialmente vazias. Como estamos interessados em estudar os metais, vamos considerar apenas os casos onde as bandas são parcialmente preenchidas.Se a n-ésima banda está parcialmente preenchida, os orbitais ocupados e os orbitais vazios da primeira zona de Brillouin são separados pela superfície de Fermi, que é definida como , onde a energia de Fermi, , é a mais alta energia para a qual existe um estado ocupado.Um modelo simples para superfície de Fermi, o gás de elétrons livre, é obtido negligenciando os efeitos da não uniformidade do potencial sentido pelos elétrons na banda de condução. A energia de cada elétron é dada pela energia de partícula livre[1]:onde estados de baixa energia preenchem uma esfera perfeita quando a temperatura é igual a zero; a superfície de Fermi é esférica. Para a maioria dos metais essa é uma ótima aproximação para a superfície de Fermi, especialmente pra metais monovalentes, onde a esfera de Fermi encontra-se totalmente na primeira zona de Brillouin.
Construção da superfície de Fermi[editar | editar código-fonte]
-
A Figura mostra as três primeiras zonas de Brillouin para uma rede quadrada. O circulo é uma superfície de energia constante para elétrons livres e corresponde a superfície de Fermi para um certo valor da concentração de elétrons. A área total da região ocupada por elétrons no espaço recíproco depende apenas dessa grandeza e é, portanto, independente da interação dos elétrons com a rede. No caso real a superfície de Fermi depende da interação dos elétrons com a rede e, portanto, não é um circulo perfeito.
Devido a inconveniência de se representar as regiões da superfície de Fermi que pertencem a mesma zona em diferentes partes do gráfico, utiliza-se o esquema de zona reduzido. A Figura mostra a superfície de Fermi de elétrons livres da Figura no esquema de zonas reduzido.
As regiões sombreadas representam estados ocupados por elétrons. Partes da superfície de Fermi se estendem até a segunda, terceira e quarta zonas. A quarta zona não está representada na figura, a primeira zona está totalmente ocupada.
Para passar das superfícies de Fermi de elétrons livres para elétrons quase livres de forma quantitativa é necessário a realização de complexos cálculos matemáticos, porém existe uma uma maneira qualitativa de se prever as formas das superfícies de Fermi para elétrons quase livres, levando em consideração os seguintes fatos:
- A interação do elétron com o potencial periódico da rede dá origem a zonas proibidas nos limites da zona de Brillouin.
- Quase sempre a superfície de Fermi intercepta os limites das zonas perpendicularmente.
- O potencial da rede arredonda os vértices das superfícies de Fermi.
- O volume total contido na superfície de Fermi não depende dos detalhes da interação com a rede, mas depende quase exclusivamente da concentração de elétrons.
As superfícies de Fermi para elétrons livres podem ser construídas usando o método de Harrison. Nele são determinados os pontos de rede reciproca e uma esfera de elétrons livres, de raio apropriado para a concentração de elétrons, é traçada com centro em cada um desses pontos. Qualquer ponto do espaço reciproco que esteja no interior de pelo menos uma esfera corresponde a um estado ocupado na primeira zona. Os pontos que estão no interior de pelo menos duas esferas correspondem a estados ocupados da segunda zona e assim por diante.
- A Figura mostra as três primeiras zonas de Brillouin para uma rede quadrada. O circulo é uma superfície de energia constante para elétrons livres e corresponde a superfície de Fermi para um certo valor da concentração de elétrons. A área total da região ocupada por elétrons no espaço recíproco depende apenas dessa grandeza e é, portanto, independente da interação dos elétrons com a rede. No caso real a superfície de Fermi depende da interação dos elétrons com a rede e, portanto, não é um circulo perfeito.Devido a inconveniência de se representar as regiões da superfície de Fermi que pertencem a mesma zona em diferentes partes do gráfico, utiliza-se o esquema de zona reduzido. A Figura mostra a superfície de Fermi de elétrons livres da Figura no esquema de zonas reduzido.As regiões sombreadas representam estados ocupados por elétrons. Partes da superfície de Fermi se estendem até a segunda, terceira e quarta zonas. A quarta zona não está representada na figura, a primeira zona está totalmente ocupada.Para passar das superfícies de Fermi de elétrons livres para elétrons quase livres de forma quantitativa é necessário a realização de complexos cálculos matemáticos, porém existe uma uma maneira qualitativa de se prever as formas das superfícies de Fermi para elétrons quase livres, levando em consideração os seguintes fatos:
- A interação do elétron com o potencial periódico da rede dá origem a zonas proibidas nos limites da zona de Brillouin.
- Quase sempre a superfície de Fermi intercepta os limites das zonas perpendicularmente.
- O potencial da rede arredonda os vértices das superfícies de Fermi.
- O volume total contido na superfície de Fermi não depende dos detalhes da interação com a rede, mas depende quase exclusivamente da concentração de elétrons.
As superfícies de Fermi para elétrons livres podem ser construídas usando o método de Harrison. Nele são determinados os pontos de rede reciproca e uma esfera de elétrons livres, de raio apropriado para a concentração de elétrons, é traçada com centro em cada um desses pontos. Qualquer ponto do espaço reciproco que esteja no interior de pelo menos uma esfera corresponde a um estado ocupado na primeira zona. Os pontos que estão no interior de pelo menos duas esferas correspondem a estados ocupados da segunda zona e assim por diante.
Medidas experimentais envolvendo a superfície de Fermi[editar | editar código-fonte]
-
A superfície de Fermi nos metais é uma prova de que os elétrons no sistema podem ser tratados através da teoria de quase-partículas.
Foi analisado nas seções anteriores que esta superfície é crucial para o entendimento de propriedades térmicas, magnéticas, elétricas e ópticas. Neste sentido, experimentalmente é necessária a existência de ferramentas específicas de modo a elucidar quais os materiais existentes ou mesmo descobrir quais são os formatos da superfície de fermi de determinado composto.
Neste sentido, existem diversas técnicas, como a aplicação do efeito De Haas-van Alphen Effect entre outras que pautam pela utilização de altos campos magnéticos para que ocorra a diferenciação de períodos de oscilação e assim possa-se medir indiretamente o modo com o qual os estados ocupados do material e portanto podendo inferir na superfície de Fermi.
Atualmente, duas técnicas tem tido destaque para se resolver as superfícies de fermi: ARPES, espectroscopia de fotoemissão angularmente resolvida, e STM, microscópio de tunelamento.
- A superfície de Fermi nos metais é uma prova de que os elétrons no sistema podem ser tratados através da teoria de quase-partículas.Foi analisado nas seções anteriores que esta superfície é crucial para o entendimento de propriedades térmicas, magnéticas, elétricas e ópticas. Neste sentido, experimentalmente é necessária a existência de ferramentas específicas de modo a elucidar quais os materiais existentes ou mesmo descobrir quais são os formatos da superfície de fermi de determinado composto.Neste sentido, existem diversas técnicas, como a aplicação do efeito De Haas-van Alphen Effect entre outras que pautam pela utilização de altos campos magnéticos para que ocorra a diferenciação de períodos de oscilação e assim possa-se medir indiretamente o modo com o qual os estados ocupados do material e portanto podendo inferir na superfície de Fermi.Atualmente, duas técnicas tem tido destaque para se resolver as superfícies de fermi: ARPES, espectroscopia de fotoemissão angularmente resolvida, e STM, microscópio de tunelamento.
ARPES - Espectroscopia de fotoemissão resolvida em ângulo[editar | editar código-fonte]
-
A técnica ARPES é baseada no efeito fotoelétrico, explicado em 1905 por Einstein através do conceito de quanta de energia.
Neste efeito, os elétrons de um material podem absorver um fóton e serem ejetados se a energia do respectivo fóton é maior que a função trabalho do material.
O ARPES funciona da seguinte forma: Uma linha de radiação branca é produzida, através da utilização de um monocromador uma determinada linha é selecionada, esse comprimento de onda é então iluminado em uma amostra. Um detector então analisa os fotoelétrons emitidos pela amostra registrando a energia e o ângulo de incidência do feixe. As resoluções atuais são de aproximadamente 2 meV e 0,2° em sofisticados experimentos feitos em síncrotrons ao redor do mundo.
Ao se registrar os ângulos e as energias, é possível através da conservação de energia e do momento da onda nas direções paralela e perpendicular, registrar o valor de V0 que é a distância da energia de Fermi ao nível do vácuo. Fazendo-se um mapa para diversos vetores de onda k, é possível construir um mapa da superfície de Fermi.
Uma das maiores desvantagens da técnica ARPES é a falta de uma informação da superfície de fermi do material como um todo, pois somente é possível a análise de determinadas direções de uma só vez, e devido ao tempo de aquisição das medidas, não é possível garantir que as distribuições eletrônicas permaneçam constantes por longos intervalos temporais.
-
-
-
-
-
-
-
-
-
- A técnica ARPES é baseada no efeito fotoelétrico, explicado em 1905 por Einstein através do conceito de quanta de energia.Neste efeito, os elétrons de um material podem absorver um fóton e serem ejetados se a energia do respectivo fóton é maior que a função trabalho do material.O ARPES funciona da seguinte forma: Uma linha de radiação branca é produzida, através da utilização de um monocromador uma determinada linha é selecionada, esse comprimento de onda é então iluminado em uma amostra. Um detector então analisa os fotoelétrons emitidos pela amostra registrando a energia e o ângulo de incidência do feixe. As resoluções atuais são de aproximadamente 2 meV e 0,2° em sofisticados experimentos feitos em síncrotrons ao redor do mundo.Ao se registrar os ângulos e as energias, é possível através da conservação de energia e do momento da onda nas direções paralela e perpendicular, registrar o valor de V0 que é a distância da energia de Fermi ao nível do vácuo. Fazendo-se um mapa para diversos vetores de onda k, é possível construir um mapa da superfície de Fermi.Uma das maiores desvantagens da técnica ARPES é a falta de uma informação da superfície de fermi do material como um todo, pois somente é possível a análise de determinadas direções de uma só vez, e devido ao tempo de aquisição das medidas, não é possível garantir que as distribuições eletrônicas permaneçam constantes por longos intervalos temporais.
 [EQUAÇÃO DE DIRAC].
[EQUAÇÃO DE DIRAC].
 + FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE
 + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO. + ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL ![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8) FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA ENERGIA DE PLANCK
ENERGIA DE PLANCK

 de energia de maneira a realizarem a transição a outro estado disponível.
de energia de maneira a realizarem a transição a outro estado disponível.














![{\displaystyle P(\mathbf {s} )={\frac {e^{-\beta H(\mathbf {s} )}}{Z}}\qquad Z=\int _{[-\pi ,\pi ]^{\Lambda }}\prod _{j\in \Lambda }d\theta _{j}\;e^{-\beta H(\mathbf {s} )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71ef5f2950de7a5f4eb1d1eacee3cd891b7ea028)

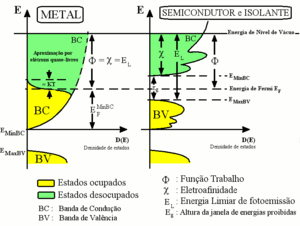























![{\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80462a105fffc6a82aab94ce41c209b37211f333)









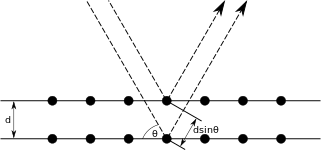
















![{\displaystyle n(x)=\sum _{p>0}^{}[C_{p}\cos {\frac {2\pi px}{a_{1}}}+S_{p}\sin {\frac {2\pi px}{a_{1}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11fb9c2bbc10893ed96c5c79543a66083fd96631)






![{\displaystyle n(x)=\sum _{p=-\infty }^{\infty }[n_{p}e^{\frac {i2\pi px}{a_{1}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edd84870ee29dab5046c2888be1255f0b5fcece4)



![{\displaystyle [n_{p}e^{\frac {i2\pi px}{a_{1}}}+n_{-p}e^{\frac {-i2\pi px}{a_{1}}}]=2Re[n_{p}]\cos {\frac {i2\pi px}{a_{1}}}-2Im[n_{p}]\sin {\frac {i2\pi px}{a_{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8837215b07993672d16f5f241d9aaeef9dccb7bf)